“How Much is That?“ is an activity I created for the 4th graders studying money. Students roll the dice to determine the number of quarters, dimes, nickels and pennies. The total value of all of the coins is then calculated. The same coins are then used to make different $1.00 combinations.
It was interesting to see the strategies used to find the total value of the coins. A handful of students drew each of the coins and then used the drawing to find the total value (i.e. circling coins that make $1.00). Most used the standard algorithm. One student employed a slightly different approach in her solution, first chunking coins together (i.e. the quarters with the dimes and the nickels with the pennies) before finding the total value. She then went on to justify her work by recording the totals for each type of coin.
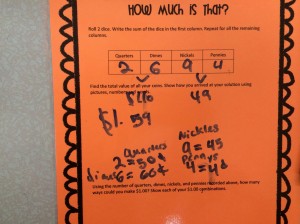Reflecting on that particular lesson nearly 2 weeks ago (it’s been a bit hectic with all of the Jewish holidays ), I started to wonder whether or not this student would have applied the same strategy if the value of her quarters was $0.75, $1.25 or $1.75. My guess is yes! This student was one of the few who demonstrated flexibility, embraced the openness of the $1.00 question, and persevered to find multiple solutions based on her coins. (There were additional solutions on a second whiteboard.)
Most students were entirely perplexed by the openness, uncomfortable with finding multiple solutions. Isn’t the question answered when one solution is found? With some encouragement and guidance from the classroom teacher, myself, and several successful classmates, most students were able to find multiple solutions.
It’s definitely time for more open-ended questions in this classroom!
Adrienne 🙂
The Math Nook 